Network science는 실제 네트워크 속성을 재현하는 모델을 구축하는 것을 목표로 합니다. 우리가 접하는 대부분의 네트워크들은 규칙성이나 예측 가능한 구조가 아닙니다. 처음에는 무작위로 회전된 것처럼 보입니다. Random network theory는 truly random 한 특성을 보이는 네트워크를 구성하고 특성화함으로써 명백한 무작위성을 수용하는 것입니다.
Random network theory embraces this apparent randomness by constructing and characterizing networks that are truly random.
실제 시스템의 복잡성을 재현할 수 있도록 하기 위해서는 노드 사이에 링크를 배치할 위치를 결정해야합니다. 이와 관련하여 Random network 철학은 무작위로 링크를 배치하면 가장 잘 목표를 달성할 수 있다고 가정합니다.
Defining Random Networks
2가지의 random network에 대한 정의
- \(G(N, L)\) Model : N개의 labeled node 들이 random 한 위치에 존재하는 link들로 이어져있다(Erdős and Rényi used their string of papers).
- \(G(N,p)\) Model : 각각의 labeled nodes가 확률 \(p\)로 연결되어 있다(model introduced by Gilbert).
Random Networks 구성단계
- N개의 isolated nodes로 시작
- Node 쌍을 선택하고 0~1 사이의 난수를 생성하여 숫자가 p보다 크면 해당 Node의 쌍을 link로 연결, p보다 작으면 그대로
- 총 N(N-1)/2번 각 Node들의 쌍에 대해 2번을 반복
이러한 과정을 거쳐 얻은 네트워크를 Random Network 혹은 Random Graph라고 하며 the Erdős-Rényi network라고 부른다.
Number of Links
N과 p가 주어졌을대 생성되는 network는 매번 다르지만 생성되는 link 개수를 예측하는 것은 매우 유용하게 사용될 수 있다.
Random network가 정확하게 \(L\)개의 link를 갖고 있다고 하면 확률을 아래 3가지 term들의 곱으로 나타낼 수 있다.
- N(N-1)/2 쌍의 Node들이 p의 확률로 link를 생성하기 때문에 \(p^L\)
- 위에서 L개의 쌍을 제외한 나머지쌍들은 1-p의 확률로 node들을 생성하기 않기 때문에 \((1-p)^{N(N-1)/2 - L}\)
- Combination factor \({N(N-1)/2\choose L}\)

여러 가지 그래프의 구조들에 따라 공식이 달라집니다.
Degree Distribution
\(p_k)\는 node가 k개의 degree를 같게 되는 확률이다.
\(p_k)\의 확률 분포는 아래와 같다. Binomial과 Poisson은 서로 근사되기 때문에 동일한 속성을 갖지만 이항 분포가 p, N에 의존하지만 Poisson은 k에만 의존하기 때문에 Poisson가 선호된다.
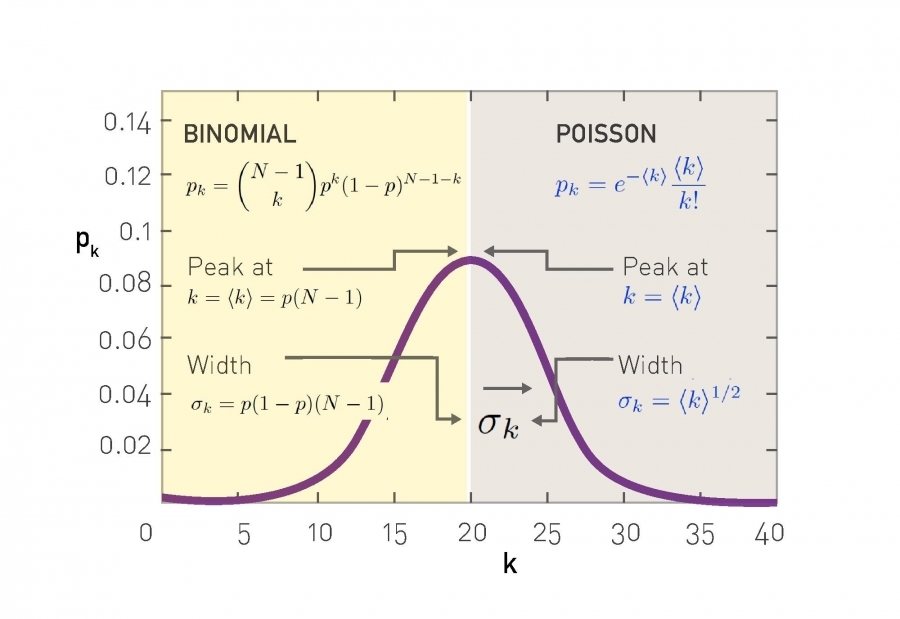
하지만 실제 현실 network는 위와 같이 Poisson이 아니다. Random Network 분산을 계산해보면 다소 좁은 범위로 계산이 되는데 현실은 다르기 때문이다. 왜냐하면 실제에서는 인기 있는 사람이 있고 인기가 없는 사람도 있지만 Random network는 모두를 동일하게 바라보기 때문이다.
본 내용은 아래 링크 내용 일부를 요약 정리한 것입니다.
http://networksciencebook.com/chapter/3
Network Science by Albert-László Barabási
The power of network science, the beauty of network visualization.
networksciencebook.com
'GraphMining' 카테고리의 다른 글
| Kronecker Graph Model (0) | 2022.09.26 |
|---|---|
| Community Guided Attachment & Forest Fire Model (0) | 2022.09.26 |
| Basic Models (0) | 2022.09.14 |
| Structural properties (2) | 2022.09.14 |
| Intro & Basic Concepts (0) | 2022.09.06 |
