KAIST AI 대학원 신기정 교수님의 수업인 데이터마이닝 및 소셜 네트워크 분석 수업 필기입니다.
Kronecker Graph Model
Self-similarity를 통한 recursive model => Power law, real-world graph structure
hyperparameter에 민감하지 않고 stably Graph를 생성
Recursive graph

Adjacency matrix간의 Kronecker Product을 통해 Graph 생성
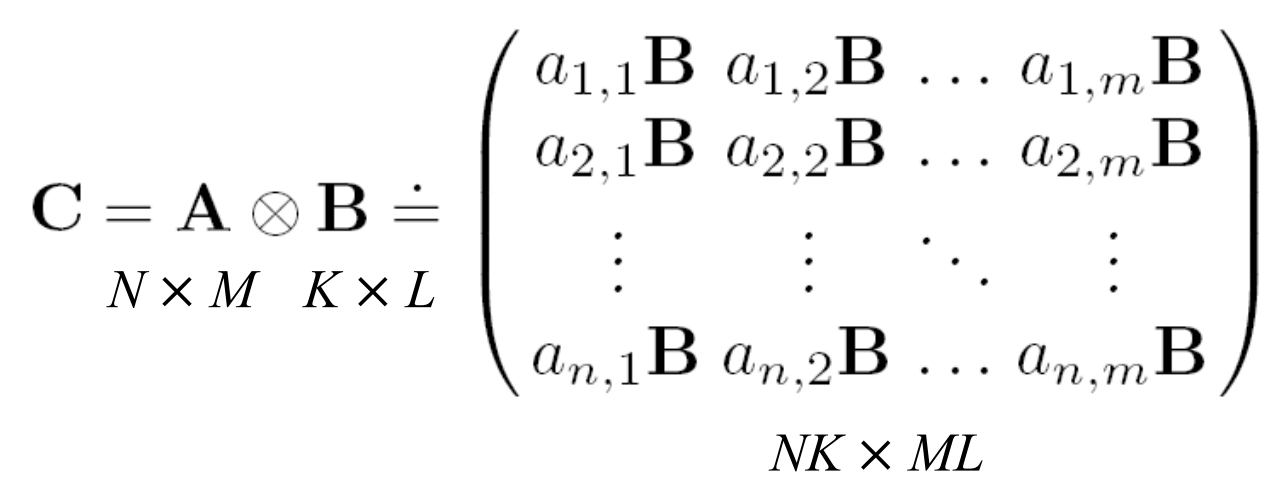
\(G_k\)가 \(G_1\)의 k times의 Kronecker product라고 할 때 \(G_k\)는 \(N_1^k\) node와 \(E_1^k\) edges를 갖게 된다.
즉, Constant diameter가 되게 된다. 이를 해결하기 위한 것은 Stochastic Kronecker graph
Stochastic Kronecker graph
shrinking diameter로 만들기 위해서 probability matrix \(P_1\)를 만들어 recursive graph를 생성한다

Conclusion
- Properties of static networks
- Power Law Degree Distribution
- Power Law eigenvalue and eigenvector distribution
- Small Diameter
- Properties of dynamic networks
- Densification Power Law
- Shrinking/Constant Diameter
Fitting Kronecker Graphs

- \(G\) : real graph
- \(\theta\) : seed graph

\(\theta\)가 link 생성 확률이기 때문에 실제 그래프 \(G\)와 비교해서 \(G[u,v]\)가 1이면 \(\theta[u,v]\)의 값으로 0이면 \(1-\theta[u,v]\)의 확률들을 모두 곱한 값으로 \(P(G\mid\theta)\)를 계산한다.
Challenge
- Node correspondence problem : 옵티마이즈 문제
-> Metroplis sampling(trial and error) - Scalability : 너무 커서 너무 느림
-> approximation of the likelihood
'GraphMining' 카테고리의 다른 글
| Basic GNN 설명 (0) | 2022.12.13 |
|---|---|
| K-Core & Katz index (1) | 2022.10.07 |
| Community Guided Attachment & Forest Fire Model (0) | 2022.09.26 |
| Basic Models (0) | 2022.09.14 |
| Structural properties (2) | 2022.09.14 |
