Iterative Deep Graph learning for Graph Neural Networks

Abstract

이 논문에서는 Iterative Deep Graph learning for Graph Neural Networks(IDGL)이라는 새로운 end-to-end graph learning framework를 제안한다.

 

IDGL은 iteratively learning과 graph embedding이 결합된 방법으로 더 나은 node embedding을 기반으로 더 나은 graph-structure을 학습할 수 있다(그 반대도 가능).

 

IDGL의 특징을 4가지 정도 이야기하는데 다음과 같다.

• Iterative method가 downstream prediction task에 충분히 최적화되면 dynamically stop 한다.
• Graph learning problem을 similarity metric learning problem로 캐스팅 한다.
• Learned Graph의 quality를 위해서 regularization을 활용한다.
• Anchar-based approximation 기술을 이용하여 time, space-complexity를 줄인 IDGL-ANCH를 제시한다.

 

Introduction

최근 몇년간 Node classification, Graph classification, Graph generation 분야에서 더 효과적인 GNN 방법들이 제시되었다. 하지만 GNN들에는 2가지 한계가 존재했는데 첫번째 문제는 Graph의 Embedding이 비슷해지는 Graph-Oversmoothing이다. 즉, Graph는 결국 Embedding vector로 변환되어 사용되는데 Embedding vector들이 유사해지는 현상을 의미한다. 두번째는 Real-world의 Graph는 noisy하거나 incomplete하다는 것이다. 따라서 본 논문은 이 2가지 한계를 어느정도 개선하는 새로운 Framework인 Iterative Deep Graph learning for Graph Neural Networks(IDGL)를 제시한다.

 

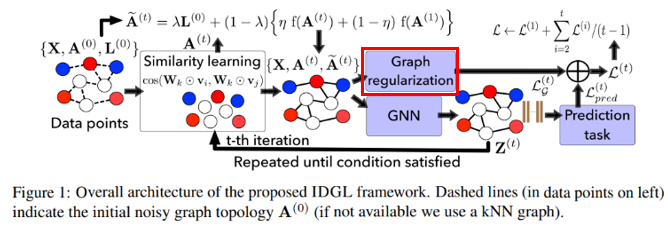
Figure 1에서 보이듯이 Embedding vector Z가 Similarity learning으로 돌아가 iteration이 진행되는 것을 볼 수 있다. 이는 Graph Structure를 Downstream task에 맞춰 필요없는 noise를 제거하는 방법이다. 또한, Figure 1에서는 2가지의 regularization이 사용되는 것을 확인할 수 있다. Graph regularization, Prediction task regularization이다. 이를 통해 Over-smoothing 문제를 개선한다.

 

IDGL Framework

IDGL은 중요한 가정을 갖고 시작하는데 초기 Graph가 noise하다는 것과 Graph의 feature matrix는 noiseless하다는 것이다. 추후 연구로 feature matrix까지 noise한 경우를 고려해야한다고 이야기한다.

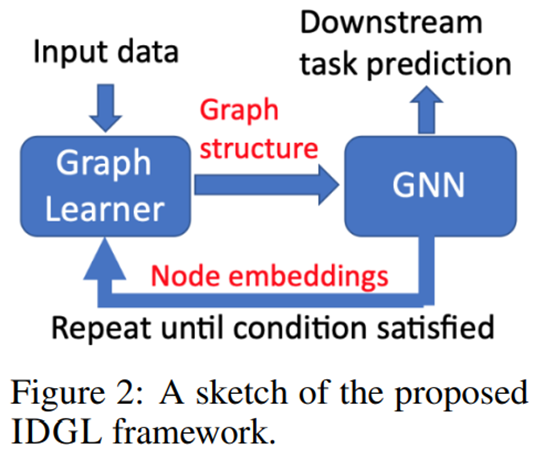
IDGL의 핵심 방법은 Iterative method이다. 따라서 본 논문에서는 아래와 같이 표현한다.

To learn a better graph structure based on better node embeddings
To learn better node embeddings based on a better graph structure

Iterative method에서 stop condition은 downstream task에 대해서 graph가 충분히 최적화되어 변화가 기준치보다 작게 발생할때로 정의한다.

 

Graph Learning as Similarity Metric Learning

Similarity Learning은 첫번째 Iteration일때는 Embedding Space Z가 없기 때문에 Feature Matrix X를 이용하여 Adjacency Matrix A와 함께 Weigted Cosine Similarity를 계산한다. 이를 통해 t기의 \(A^{(t)}\)를 생성한다. 두번째 Iteration부터는 Embedding Space Z를 이용하여 진행한다.

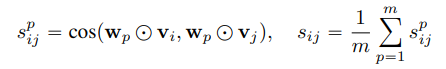
Similarity Learning에서 Weigted Cosine Similarity의 범위가 -1부터 1까지 나오게된다. 하지만 Adjacency Matrix A는 기본적으로 non-negative를 가정하기 때문에 s가 음수인 것을은 계산에서 제외하게된다. 즉, s가 음수가 나온다는 것은 noise하다고 생각하고 제외한다고 해석할 수 있다. 이러한 방법을 \(\epsilon\)-neighborhood라고 한다.

 

Graph Node Embeddings and Prediction

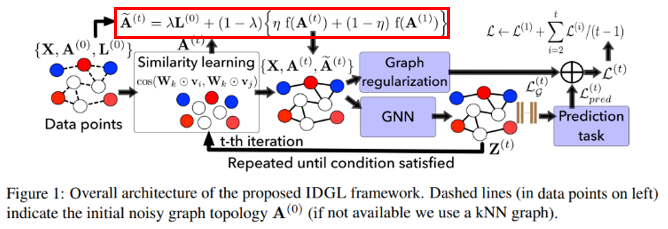
다음은 optimized graph structure인 \(\tilde{A}\)를 얻는 것이다. \(\tilde{A}\)는 Laplacian Matrix L, row normalized adjacency matrix \(f(A)\)와 초기 adjacency matrix \(A^{(1)}\)를 \(A^{(t)}\)와 합성하여 만들어진다.

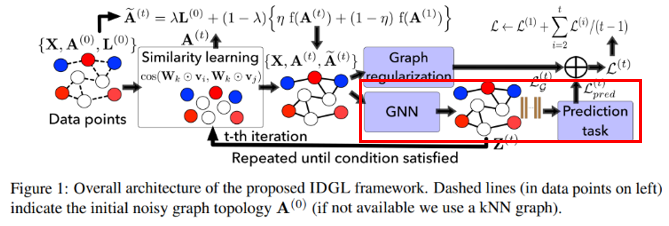
이후 GNN State를 거치게된다. IDGL의 GNN은 two-layered GCN을 사용한다. 첫번째 Layer은 Raw node feature X를 intermediate embedding space로 mapping하는 역할을한다.

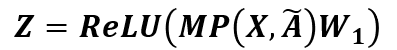
첫번째 Layer의 결과 값인 Z는 다시 Similarity Learning으로 돌아가 Stop condition을 충족할때까지 Iteration을 하게된다.

 

두번째 Layer는 intermediate node embedding Z를 Output Space로 mapping하는 역할을 한다.

따라서 두번째 Layer의 결과값은 Downstream task에 대한 예측값이된다. 이를 통해 우리는 \(\hat{y}, y\)의 Loss를 구할 수 있다. 이어서 설명할 Graph Regularization Loss와 함께 사용된다.

 

\(MP(F,\tilde{A}) = \tilde{A}F\)

 

Graph Regularization

Graph Regularization Loss는 크게 2가지 term으로 나뉘는데 첫번째는 Dirichlet energy이다.

Dirichlet energy는 Graph의 Smoothness를 control하는 term으로 graph가 첫 graph에 대한 속성들을 잃지 않도록 하는 것의 목표이다.

위의 식을 해석하면 Laplacian Matrix L를 Feature Matrix X에 대해서 Decomposition하여 Eigenvalue들을 모두 더한 것이다. 즉, A와 X에 의 유사성이라고 이야기할 수 있다. 예를들어 A와 X가 유사하다면 Dirichlet energy는 작아질 것이고 A와 X가 상이하다면 Dirichlet energy는 커질 것이다. 우리는 Dirichlet energy를 Minimizing하는 것을 목표로한다. Feature Matrix X는 초기 Graph의 속성을 갖고 있기 때문에 A가 변화하더라도 이를 잃지 않게 하는 것이 목표이다.

 

두번째 term은 Graph의 Sparse를 Control하기 위한 term이다.

 \(f(A)\)의 첫번째 term은 disconnected graph에 대해 penalty를 주는 것에 목적이 있다. 두번째 term은 첫번째 term을 규제하는 것에 목적이 있다. 왜냐하면 첫번째 term만 존재한다면 매우 spare한 graph가 생성되기 때문이다(그렇다고 합니다..!).

 

우리는 최종적으로 2가지의 term을 합쳐 Graph Regularization Loss로 사용합니다.

이를 다시 Task-depndent prediction loss와 합쳐 IDGL의 총 Loss로 사용하게된다.

 

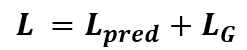
IDGL Sudo Code

위의 Sudo Code를 보면 Model에 대한 이해가 더 쉬울 것 같습니다.

따로 IDGL-ANCH는 살펴보지 않습니다. 왜냐하면 Sampling이나 Message Passing 과정에서 Approximation을 사용한 것이 전부이기 때문에 함께 설명하면 본 Model에 대해 햇갈릴 것 같기 때문입니다.

 

Experiment

Datasets

Graph datasets

• Cora
• Citeseer
• Pubmed
• Ogbn-arxiv

Non-graph datasets

• Wine
• Breast Cancer
• Digits

Text datasets

• 20Newsgroups data
• movie review data

Graph dataset과 Non-Graph dataset은 Node classification을 진행합니다. 그리고 Text datasets은 Graph-level prediction을 진행합니다. Non-graph dataset과 Text datasets은 graph가 없기 때문에 KNN graph algorithm을 이용하여 Graph를 생성하여 진행합니다.

 

Classification accuracies on transductive

거의 대부분의 Dataset에 대해서 가장 우수한 결과를 보였습니다.

 

Classification accuracies on inductive

심지어 Text dataset에서도 좋은 결과를 보였습니다.

즉, IDGL은 다양한 Dataset에서도 꾸준히 좋은 성능을 보인다는 것을 확인할 수 있었습니다.

 

Ablation study on various node/graph classification datasets

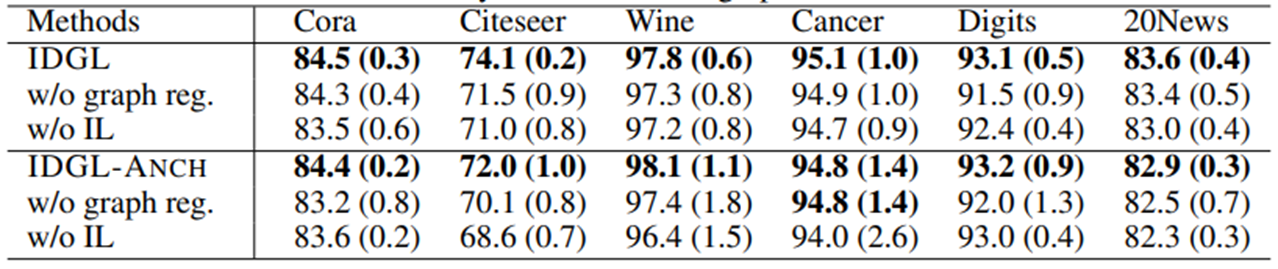
Graph Regularization과 Iterative Learning이 최종 performance에 좋은 영향을 주었는지를 확인하기 위해서 각각을 제외하고 진행해본 결과 두개를 모두 사용한 경우가 결과가 좋게 나왔습니다.

 

Evaluate the robustness of IDGL to adversarial graph

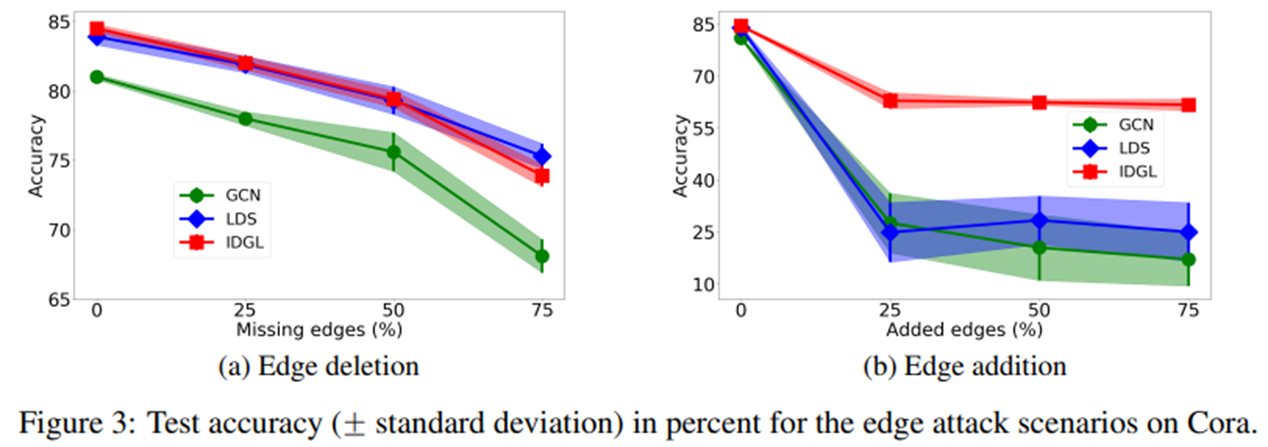
다음은 Edge를 무작위로 추가하거나 삭제했을때 성능의 변화를 살펴보았습니다. IDGL은 다른 Baseline Model에 비해 무작위로 Edge를 deletion할때 나쁘지 않은 모습을 보였습니다. LDS와는 거의 비슷한 추세를 보였습니다. 하지만 무작위로 Edge를 Addition하였을때는 매우 Robust한 성능을 보였습니다. 즉, IDGL은 noise한 data에 대해서 매우 robust하다는 사실을 확인할 수 있습니다.

 

Evolution of the learned adjacency matrix and accuracy through iterations

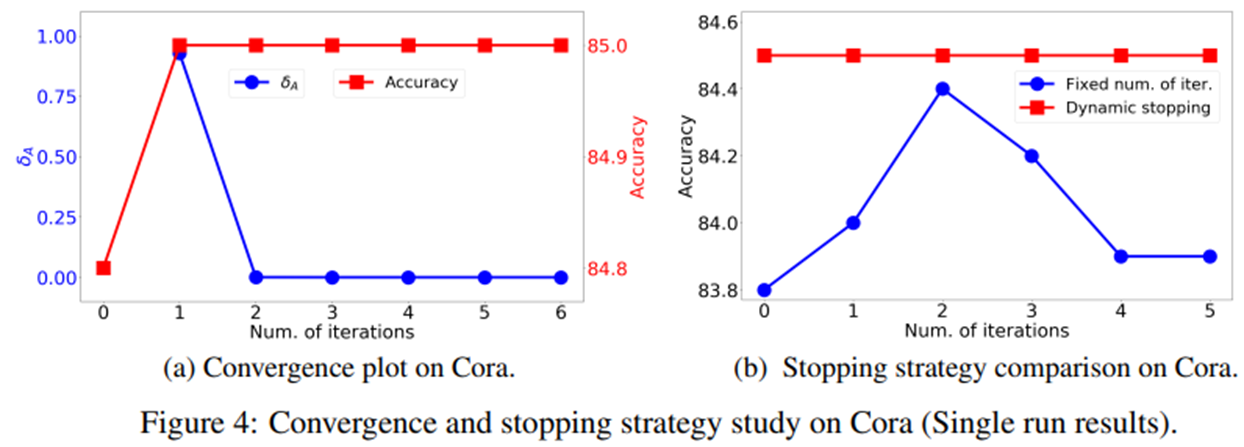
그러면 얼마나 Iteration을 해야할지에 대한 부분을 확인해보기 위해서 Iteration 횟수에 따른 Adjacency matrix의 변화를 살펴보았습니다 Figure 4에서 a를 보면 첫번째 Iteration에서 변화가 대부분 일어나는 것을 확인할 수 있습니다. Figure 4에서 b는 횟수를 고정시켜 놓고 Iteration을 시킨 것인데 2번정도 하였을때 Dynamic stopping을 하였을 때와 비슷한 결과를 보입니다. 따라서 Iteration을 많이 할 필요가 없다는 것을 암시합니다.

 

감사합니다:)