Autoencoder의 모든 것 - 이활석(NAVER) 을 정리한 것입니다.
https://www.youtube.com/watch?v=rNh2CrTFpm4
Autoencoder의 주요 목적은 Manifold가 목적이다. 따라서 Encoder를 잘하는 게 핵심이다.
반면, Variational Autoencoder(VAE)는 학습을 통해 생성(Generative)이 목표이다. 따라서 Decoder(Generator)가 핵심이다.
VAE은 Generative Model이다.
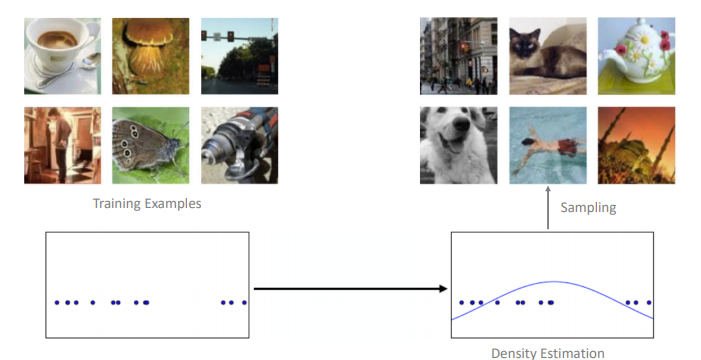
VAE의 목적은 Sample Data를 통해 결국 새로운 Data를 Generative(생성)하는 것이다.
Generative Model
우리의 목적은 x를 추정하는 probability를 최대화 하는 것이다.
즉, 우리의 Target인 x가 최대화 되는 점을 찾기 위해서 MLE를 사용하게 된다.
아무것도 없는 상태에서 새로운 것을 창조하기 어렵기 때문에 train data라는 sample을 Condition으로 주고 그것을 토대로 새로운 것을 생성하는 것이다.

\(z\)값의 분포는 Simple Distribution로 가정했기 때문에 \(p(z)\)는 Random Variable이다.
\(g_\theta(*)\)는 확률분포의 파라미터를 추정하는 Deterministic Function이다.
\(p(x|g_\theta(z))=p_\theta(x|z)\) z를 주었을 때 x에 대한 Likelihood를 알 수 있게 된다.
우리는 z 값이 주어졌을 때 \(g_\theta()\)를 통해 확률분포를 알 수 있게 되고, \(p(z)\)를 알기 때문에 둘을 곱한 것을 적분하여 최종적으로 우리가 알고 싶은 Maximum 된 \(p(x)\)를 구할 수 있게 된다.
Prior Distrubution P(z)?
이때 Latent Variable의 확률분포는 Latent Variable이 일종의 Controller 역할을 할 수 있도록 다루기 쉬운 확률분포를 이용한다.
우리가 Manifold 한 값이 매우 고차원적이고 복잡할 것 같은데, Simple Distribution으로 가정하는 게 합리적인가?
상관없다. 왜냐하면 우리가 하는 것은 결국 딥러닝이기 때문에 Simple Distribution을 사용해도 앞에 있는 몇 개의 Layer들이 Manifold를 잘 찾을 수 있다.
Direct MLE?
적분하는 것 말고 Sample 여러 개 모아서 더해서 바로 사용하면 되지 않나요?
안된다. 아래의 (b)는 (a)에서 앞부분을 약간 지운 것이고, (c)는 (a)를 한 픽셀을 옆으로 이동시킨 것이다. 의미적으로는 (c)가 (a)와 더 가깝지만, MSE는 (b)보다 (c)가 더 크다. 이처럼 현실적으로 올바른 확률 값을 구하기 어렵기 때문에 maximum likelihood estimation을 directly 사용해서는 안된다.

Variational Inference
MLE를 직접 사용하면 위에서 설명한 것과 같은 문제가 발생하기 때문에 우리는 Variational Inference라는 방법을 사용하게 된다.

z를 의미적으로 가장 가깝게 추정하는 어떤 이상적인 Sampling 함수 p(z|x)를 가정한다. 이것은 prior 함수는 아니고 x를 알려주고 적어도 x는 잘 Generative 하는 함수이다. 이 함수를 우리는 모르기 때문에, Variation Inference를 사용한다. 우리가 추정하고 싶은 True posterior에 가장 유사한 분포를 사용하는 것이다.

- \(p(z|x)\) : 이상적인 함수
- \(q_\theta(z|x)\) : 이상적인 함수를 근사하는 함수로 Generative 하는 데 사용할 함수
ELBO : Evidence LowerBOund
Relationship among \(p(x)\), \(p(z|x)\), \(q_\theta(z|x)\): Derivation 1

Jensen’s Inequality를 사용하여서 ELBO를 찾는 방법이다.
Relationship among \(p(x)\), \(p(z|x)\), \(q_\theta(z|x)\): Derivation 2

p(x)에 log를 씌우면 최종적으로 2가지 term이 나오게 된다. 위 그림에서 앞의 term이 ELBO term이고, 뒤의 term이 KL term이다. KL을 최소화하는 것은 ELBO를 최대화하는 것과 같다.
KL은 두 확률분포 간의 거리에 대한 함수이다. 즉, KL이 최소화된다는 뜻은 우리가 이상적인 함수라고 가정했던 확률분포와 우리가 추정하고자 하는 확률분포 간의 거리가 최소가 되었다는 점이다. 우리는 p(z|x)를 모르기 때문에 ELBO를 최대화하여서 KL을 최소 하는 방법을 사용한다.

Variation Inference 관점에서 최적화된 Sampling 함수는 KL을 최소화는 것이고 이것은 ELBO를 최대화하는 것과 같다. 따라서 우리는 2가지를 Optimization 하게 된다.
- ELBO term을 Φ에 대해 maximize 하면 이상적인 sampling함수를 찾는 것이다.
- ELBO term을 𝜃에 대해 maximize 하면 MLE 관점에서 Network의 파라미터를 찾는 것이다.

*여기서 KL은 위에서 KL과 다르다!!!
Generator를 학습하고 싶은데, prior에서 sampling 하면 잘 안된다. 따라서 x를 주고 이상적인 Sampling 함수를 근사하는 \(q_\phi\)를 찾는다. 이 과정은 ELBO를 Mazimize 하는 것이다. ELBO term의 앞부분은 Sampling 함수를 이용해 x가 나오도록 MLE 하는 것이기 때문에 우리는 2가지 Optimization을 한꺼번에 할 수 있게 된다.

이제 우리는 Sampling 함수 \(q_\phi\)를 이용해서 L개를 Sampling 하여 평균을 구해서 Reconstruction Error를 구할 것인데, Sampling을 한다는 것은 Backpropagation이 안된다는 뜻이다. 따라서 우리는 Reparameterization Trick을 사용해서 이를 극복한다. 이를 사용하면 확률적인 특성은 같다.
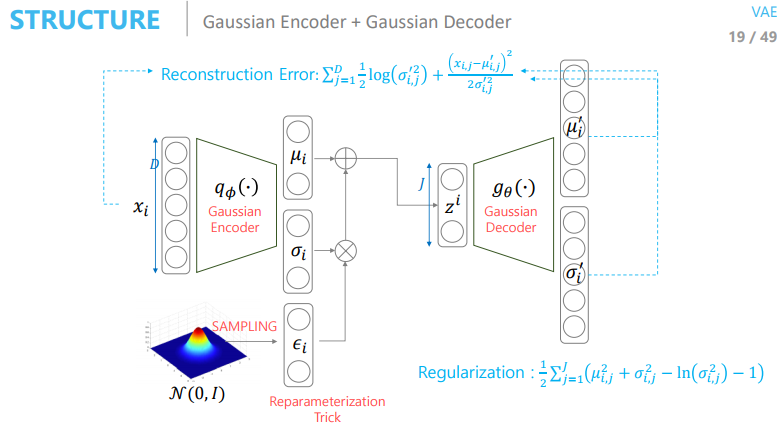
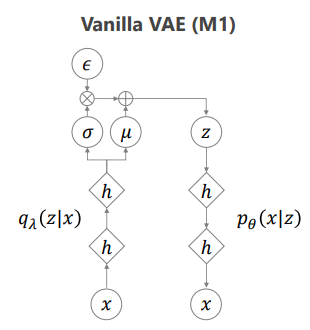
Structure

CVAE(Conditional VAE)
CVAE는 레이블 값을 Condition으로 주는 것이다. 레이블 값을 모를 때는 레이블 값을 추정하여서 Condition으로 주는 것이다.


AAE(Adversarial Autoencoder)

Encoder에서 KL term이 가우시안 말고는 계산이 안된다는 단점이 있다. 이를 극복하기 위해서 나온 것이 AAE이다. \(q_\phi\)가 p가 되도록 GAN을 이용하는 것이다. KL term을 GAN의 discriminator로 바꾸어주는 것이다.

'DL Study' 카테고리의 다른 글
| Generative Adverarial Network(GAN) (0) | 2022.09.22 |
|---|---|
| #3 Autoencoder의 모든 것 - AutoEncoder (0) | 2022.09.16 |
| #2 Autoencoder의 모든 것 - Manifold Learning (2) | 2022.09.15 |
| #1 Autoencoder의 모든 것 - 2가지 관점으로 DNN Loss 함수 이해하기 (0) | 2022.09.14 |
| LSTM(Long Short-Term Memory) (0) | 2022.09.13 |
